Explanation of Work-Energy Theorem

 Here's an explanation of the Work-Energy Theorem in 6 simple steps:

Energy: 

• Energy is a property of an object that allows it to do work or cause change. 
• There are different forms of energy, such as kinetic energy (energy of motion), potential energy (stored energy), and thermal energy (energy related to temperature).

Work: 

• Work is done when a force is applied on an object, causing it to move. 
• The amount of work done on an object is calculated by multiplying the force applied by the distance it moves in the direction of the force.

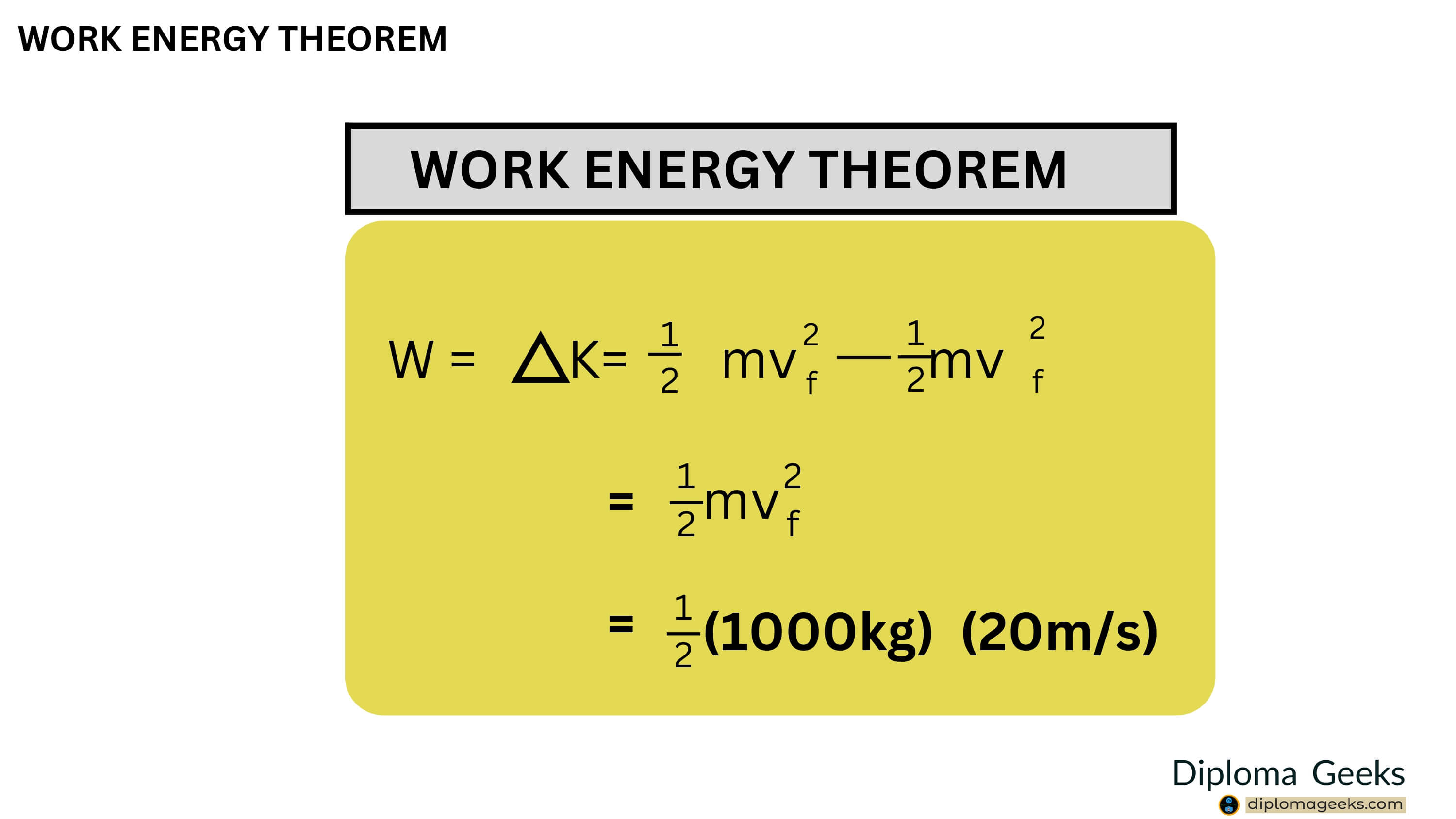
The Work-Energy Theorem: 

• The Work-Energy Theorem states that the work done on an object is equal to the change in its energy. 
• In other words, work and energy are interchangeable.

Example: 

• For example, if you lift an object to a higher height, you are doing work on it and increasing its potential energy.
• If you then drop the object, its potential energy will be converted into kinetic energy as it falls, causing it to gain speed.

Conservation of Energy: 

• The Work-Energy Theorem is related to the principle of the conservation of energy, which states that the total amount of energy in a system remains constant as long as it is not influenced by external factors.

Applications:

• The Work-Energy Theorem is used in many fields, including physics, engineering, and mechanics, to analyze and solve problems related to work and energy. 
• Understanding the theorem helps us understand how energy is transformed and used in real-world applications, such as in machines, vehicles, and everyday life.

Examples of Work and Energy

 

Work:

• Pushing a shopping cart at the grocery store is an example of work. 
• The force applied to the cart to move it is work being done.
  Turning a doorknob to open a door is another example of work.
• The force applied to the doorknob is work being done.
  

Energy:

• A rollercoaster ride is an example of energy in motion. The potential energy stored in the rollercoaster due to its height is converted into kinetic energy as it moves down the track.
• A battery-operated toy car is another example of energy in motion. The chemical energy stored in the battery is converted into kinetic energy to make the car move.
• A falling apple is an example of potential energy being converted into kinetic energy. As the apple falls, its potential energy due to its height decreases, while its kinetic energy increases.

Types of Energy: Potential and Kinetic

Energy is a property of matter that enables it to do work. Energy is an essential aspect of the universe and is found in many different forms. 

The two main types of energy are potential energy and kinetic energy.

 Potential Energy:

• Potential energy is the energy an object has due to its position or state. 
• For example, an object kept on a height has potential energy due to its height above the ground. 
• The potential energy of an object depends on its position relative to a reference point, and it increases as the object is moved further away from the reference point.

Kinetic Energy:

• Kinetic energy is the energy of motion. It is the energy an object possesses due to its motion or the speed at which it is moving. 
• The kinetic energy of an object is proportional to its mass and the square of its velocity.

 

EXAMPLES

Potential Energy: example

• A stretched rubber band has potential energy. The more it is stretched, the more potential energy it has stored.
• A book kept on a shelf has potential energy due to its height above the ground.
• A charged battery has potential energy stored in it, which can be used to power electrical devices.
  

Kinetic Energy: example

• A moving car has kinetic energy due to its motion. The faster the car moves, the more kinetic energy it has.
• A spinning ice skater has kinetic energy due to their rotation. The faster they spin, the more kinetic energy they have.
• A flying bird has kinetic energy due to its motion through the air.
  

Work and Energy - Definition of Work Definition of Energy

 Work:

• Work is defined as the transfer of energy from one point to another through the application of force. 
• Mathematically, it can be expressed as the product of the force applied and the distance moved in the direction of the force.

Energy:

• Energy is defined as the ability to do work. It is a scalar quantity and can take different forms such as kinetic energy (the energy of motion), potential energy (the energy stored in an object due to its position or state), thermal energy (the energy related to the temperature of an object), etc.

In simple terms, work is what you do, and energy is what you need to do work.

Define Sabines formula

• Sabine's formula is a tool to calculate the reverberation time of a room.
• Reverberation time is how long it takes for the sound in a room to decrease by 60 decibels after the sound source has stopped.
• The formula uses three main factors to calculate the reverberation time: the volume of the room, the total surface area of the walls, ceiling, and floor, and the average sound absorption of the room's surfaces.
• By considering these factors, the formula can predict how sound will behave in a room and how long it will linger.
• This information is useful for architects, engineers, and acousticians who design and build spaces for different purposes, such as speech, music, or theater.

Define reverberation and reverberation time

 

Reverberation:

• Reverberation is the echoing of sound within a space.
• This means that when sound waves hit surfaces, like walls, they reflect back and mix with the original sound.
• The result of this mixing is a continuation of sound even after the original sound source has stopped.
• Reverberation can affect the clarity and quality of sound, making it seem muffled or indistinct.
• It also contributes to the sense of spaciousness in a room.

Reverberation Time:

• Reverberation time is the amount of time it takes for the sound in a space to decrease by 60 decibels.
• In other words, it's a measure of how long the sound energy lasts in a room.
• This time can be influenced by various factors, such as the size, shape, and materials used in the construction of the room.
• A longer reverberation time can create a sense of spaciousness, but can also make it difficult to understand speech or other sounds.
• A shorter reverberation time can improve speech intelligibility, but can make a space seem smaller and less live.

Define echo and its applications

Echo

• An echo is a sound that is reflected off a surface and returns to the listener. 
• It is created when a sound wave travels through a medium and bounces back after hitting a surface that is capable of reflecting sound. 
• The time delay between the original sound and the reflected sound is what creates the echo.

 

In physics, echoes have a variety of applications, including:

• Sonar and radar: to determine the distance and shape of objects in the ocean or in the air.
• Acoustic testing: to evaluate the sound quality of rooms, auditoriums, and concert halls
• Wildlife management: to study the vocalizations of animals and their habitats
• Geological exploration: to map the interior of the Earth, by analyzing the echoes of seismic waves.
• Medical imaging: to examine internal organs, using ultrasound.

Define doppler effect and its application

The Doppler effect 

• It is a change in frequency or wavelength of a wave in relation to an observer who is moving relative to the source of the wave. 
• It is named after Austrian physicist Christian Doppler.

• A common example of the Doppler effect is the change in pitch of a siren on a moving ambulance. 
• As the ambulance approaches, the sound waves are compressed, causing the pitch to increase. 
• As the ambulance moves away, the sound waves are stretched, causing the pitch to decrease.

In physics, the Doppler effect is used in a variety of applications, such as:

• Sonar and radar: to measure the speed of objects, such as ships or aircraft.
• Astronomy: to measure the velocity of stars and galaxies.
• Medical imaging: to study blood flow in the human body, using ultrasound.
• Weather forecasting: to track storms, by measuring the Doppler shift of the radar signals they reflect.

Define Noise & Types of noise

Noise can be defined as unwanted or excessive sound that can cause disturbance, discomfort, or harm to human beings and other living creatures.

Types of Noise:

• a. Continuous Noise: Continuous noise is a type of noise that occurs for a long duration without interruption. Examples of continuous noise include traffic noise, construction noise, and industrial noise.
• b. Intermittent Noise: Intermittent noise is a type of noise that occurs periodically or with breaks in between. Examples of intermittent noise include car horns, sirens, and barking dogs.
• c. Impulsive Noise: Impulsive noise is a type of noise that occurs as a sudden and brief burst of sound. Examples of impulsive noise include explosions, fireworks, and gunfire.
• d. Low-Frequency Noise: Low-frequency noise is a type of noise that has a low frequency, typically below 20 Hz. This type of noise can cause discomfort, disturbance, and even health problems, especially for those who are sensitive to it. Examples of low-frequency noise include engine noise from ships and trains, and wind turbines.

Properties of Sound

 

The properties of sound are the characteristics that describe a sound wave and determine its behavior. These properties include:

a. Amplitude: 

Amplitude is a measure of the maximum displacement of a sound wave from its rest position. It is related to the loudness of a sound, with larger amplitudes resulting in louder sounds. Amplitude is measured in units such as meters or decibels.

b. Wavelength:

 Wavelength is the distance between two consecutive peaks or troughs of a sound wave. It is a measure of the size of the wave and is inversely proportional to the frequency of the wave. Wavelength is usually measured in meters.

c. Frequency: 

Frequency is the number of complete waves that pass a point in a given unit of time, usually expressed in Hertz (Hz). It is directly proportional to the speed of sound and inversely proportional to the wavelength. Higher frequency sounds have a higher pitch, while lower frequency sounds have a lower pitch.

d. Speed:

Speed is the rate at which a sound wave travels through a medium, usually expressed in meters per second (m/s). The speed of sound in a medium depends on the temperature, pressure, and density of the medium. In air, the speed of sound is approximately 340 m/s.

Define wave & Types of waves:

•  A wave is a disturbance that travels through space and time, carrying energy from one place to another without the transfer of mass. 
• Waves are characterized by their wavelength, frequency, and amplitude.

Types of Waves:

• a. Mechanical Waves: Mechanical waves are waves that require a medium to propagate, such as air or water. They are characterized by their wavelength, frequency, and amplitude, and can be either longitudinal or transverse. Examples of mechanical waves include sound waves, ocean waves, and seismic waves.
• b. Electromagnetic Waves: Electromagnetic waves are transverse waves that do not require a medium to propagate. They travel through a vacuum, such as space, and carry energy in the form of electromagnetic fields. Examples of electromagnetic waves include light, X-rays, and radio waves.
• c. Longitudinal Waves: Longitudinal waves are waves in which the displacement of the medium is in the same direction as the direction of wave propagation. Examples of longitudinal waves include sound waves and seismic waves.
• d. Transverse Waves: Transverse waves are waves in which the displacement of the medium is perpendicular to the direction of wave propagation. Examples of transverse waves include light waves and ocean waves.

Qualities of sound

 

a. Pitch:

• Pitch refers to the perceived highness or lowness of a sound, which is directly related to the frequency of the sound wave. 
• High-pitched sounds have a high frequency, while low-pitched sounds have a low frequency.

b. Duration: 

• Duration refers to the length of time a sound lasts. 
• This can be measured in seconds or any other unit of time.

c. Intensity: 

• Intensity is a measure of the energy of a sound wave, and is directly related to its amplitude.
• Intensity is usually measured in decibels (dB). High-intensity sounds are louder, while low-intensity sounds are quieter.

d. Timbre:

• Timbre is the quality of a sound that distinguishes it from other sounds with the same pitch and intensity. 
• It is related to the complexity of the sound wave and the relative strengths of different frequency components of the wave. 
• Timbre allows us to differentiate between different instruments playing the same note and at the same volume.

Definition of sound, Measurement of sound

Sound 

 

• It is a type of energy that travels through the air as a longitudinal wave, characterized by its frequency, wavelength, and amplitude.

Measurement of Sound:

• Sound Intensity: Sound intensity is defined as the power of sound per unit area, measured in watts per square meter (W/m^2). The sound intensity of a source decreases with increasing distance from the source.
• Decibel (dB): Decibels are a logarithmic unit used to express the intensity of a sound relative to a reference level. Decibels are calculated as:

dB = 10 log (I/I0)

Where:

• dB is the sound level in decibels
• I is the intensity of the sound
• I0 is the reference level of sound intensity

Equations of projectile,trajectory Position after time t, velocity after time t

 

Projectile motion

it refers to the motion of an object that is projected into the air and subject to the acceleration due to gravity. 

The equations of motion for an object in projectile motion can be described by:

Position after time t:

• x = x0 + v0t cosθ
• y = y0 + v0t sinθ - (1/2)gt^2

Where:

• x is the horizontal position of the object at time t
• y is the vertical position of the object at time t
• x0 is the initial horizontal position of the object
• y0 is the initial vertical position of the object
• v0 is the initial velocity of the object
• θ is the angle at which the object was projected
• g is the acceleration due to gravity
• t is time

Velocity after time t:
vx = v0 cosθ
vy = v0 sinθ - gt

Where:

• vx is the horizontal velocity of the object at time t
• vy is the vertical velocity of the object at time t
• v0 is the initial velocity of the object
• θ is the angle at which the object was projected
• g is the acceleration due to gravity
• t is time

 

Trajectory of a projectile 

it is a parabolic path and can be represented by the following equation:

y = y0 + v0t sinθ - (1/2)gt^2

Where:

• y is the vertical position of the object at time t
• y0 is the initial vertical position of the object
• v0 is the initial velocity of the object
• θ is the angle at which the object was projected
• g is the acceleration due to gravity
• t is time

Equations of motion in special case

 In physics, there are several special cases of motion that are described using specific equations of motion. These special cases include:

Uniform Circular Motion: 

• An object moving in a circular path at a constant speed is said to be in uniform circular motion. 
• The equation of motion for an object in uniform circular motion can be described using centripetal acceleration, which is defined as the acceleration of an object towards the center of a circle.

a = v^2/r

Where:
a is the centripetal acceleration
v is the velocity of the object
r is the radius of the circular path

Simple Harmonic Motion:

• Simple Harmonic Motion refers to the periodic motion of an object about its mean position, characterized by a sinusoidal motion. 
• The equation of motion for an object in simple harmonic motion can be described by the following equation:
• x = A cos (ωt + φ)

Where:
x is the displacement from the mean position
A is the amplitude of the motion
ω is the angular frequency of the motion
t is time
φ is the phase constant

Projectile Motion:

• Projectile motion refers to the motion of an object that is projected into the air and subject to the acceleration due to gravity. 
• The equations of motion for an object in projectile motion can be described by:

x = x0 + v0t cosθ
y = y0 + v0t sinθ - (1/2)gt^2

Where:
x is the horizontal displacement of the object at time t
y is the vertical displacement of the object at time t
x0 is the initial horizontal position of the object
y0 is the initial vertical position of the object
v0 is the initial velocity of the object
θ is the angle at which the object was projected
g is the acceleration due to gravity
t is time

Relative Motion: 

• Relative motion refers to the motion of an object relative to a reference frame. 
• The equation of motion for an object in relative motion can be described by considering the motion of the object with respect to the reference frame. 
• The equations of motion are dependent on the choice of reference frame and the relative velocity between the object and the reference frame.

Average velocities with variation in S,V

Average velocity in kinematics refers to the total displacement of an object divided by the time it takes to cover that displacement. It is a measure of the rate of change of the position of an object and can be calculated using the following formula:

V_avg = ΔS/Δt

Where:
V_avg is the average velocity
ΔS is the change in position or displacement
Δt is the change in time

In cases where the velocity of an object changes, the average velocity can be calculated as the total displacement divided by the total time it takes to cover that displacement. The average velocity can be different from the instantaneously velocity of an object at a particular moment in time.

Average Velocity with Variation in S: 

When the displacement of an object changes over time, the average velocity can be calculated by dividing the change in displacement by the change in time.

Average Velocity with Variation in V: 

When the velocity of an object changes over time, the average velocity can be calculated by taking the arithmetic mean of the initial and final velocities and dividing by 2.

V_avg = (V_initial + V_final)/2

Average Velocity with Variation in S and V: 

When both the displacement and velocity of an object change over time, the average velocity can be calculated by dividing the total displacement by the total time. This calculation takes into account both the initial velocity and the change in velocity over time.

Equations of vertical, horizontal and oblique projection

• Kinematics equations for vertical, horizontal, and oblique projection are used to describe the motion of an object that is projected into the air under the influence of gravity. 
• The equations take into account the initial velocity and direction of the object, as well as the acceleration due to gravity, to determine the position and velocity of the object at any given time.

 

Vertical Projection: 

• When an object is projected vertically upwards, it follows a parabolic path. The equation of motion for a body projected vertically upwards is
  

x = x0 + v0t - (1/2)gt^2

Where:
x is the final height of the object at time t.
x0 is the initial height from which the object was projected.
v0 is the initial velocity with which the object was projected.
g is the acceleration due to gravity (9.8 m/s^2 on the surface of the Earth).
t is the time elapsed.

Horizontal Projection:

 When an object is projected horizontally, it follows a straight line path. The equation of motion for a body projected horizontally is:
x = x0 + v0t

• Where:
• x is the horizontal displacement of the object at time t.
• x0 is the initial horizontal displacement of the object at time t=0.
• v0 is the initial horizontal velocity with which the object was projected.
• t is the time elapsed.

Oblique Projection: 

When an object is projected at an angle, it follows a path that is a combination of vertical and horizontal motion. The equations of motion for a body projected obliquely are:
x = x0 + v0t cosθ - (1/2)gt^2
y = y0 + v0t sinθ - (1/2)gt^2

Where:

• x is the horizontal displacement of the object at time t.
• y is the vertical displacement of the object at time t.
• x0 is the initial horizontal displacement of the object at time t=0.
• y0 is the initial vertical displacement of the object at time t=0.
• v0 is the initial velocity with which the object was projected.
• θ is the angle at which the object was projected.
• g is the acceleration due to gravity (9.8 m/s^2 on the surface of the Earth).
• t is the time elapsed.

Motion under gravity and equations of motion under gravity

 

a. Standard: 

The standard equation of motion under gravity is given by

x = x0 + v0t + (1/2)gt^2  Where:

• x is the final displacement of the object at time t.
• x0 is the initial displacement of the object at time t=0.
• v0 is the initial velocity of the object at time t=0.
• g is the acceleration due to gravity (9.8 m/s^2 on the surface of the Earth).
• t is the time elapsed.

b. Freely falling: 

Freely falling objects are objects that are in a state of constant acceleration due to gravity and are not subject to any other forces. The equation of motion for a freely falling object can be derived from the standard equation of motion by setting the initial velocity to zero (v0 = 0):

x = x0 + (1/2)gt^2

Where:

• x is the final displacement of the object at time t.
• x0 is the initial displacement of the object at time t=0.
• g is the acceleration due to gravity (9.8 m/s^2 on the surface of the Earth).
• t is the time elapsed.

c. Projected vertically down:

 A body projected vertically downwards is an object that is being dropped from some height and is subject to only the force of gravity. The equation of motion for a body projected vertically downwards can be derived from the standard equation of motion by setting the initial velocity to zero (v0 = 0) and the initial height to the height from which the object was dropped (x0):

x = x0 + (1/2)gt^2

Where:

• x is the final displacement of the object at time t.
• x0 is the initial height from which the object was dropped.
• g is the acceleration due to gravity (9.8 m/s^2 on the surface of the Earth).
• t is the time elapsed.

d. Projected vertically up:

 A body projected vertically upwards is an object that is being thrown upwards and is subject to only the force of gravity. The equation of motion for a body projected vertically upwards can be derived from the standard equation of motion by setting the initial velocity to the upward velocity with which the object was thrown (v0) and the final velocity to zero (v = 0):

x = x0 + v0t - (1/2)gt^2

Where:

• x is the final displacement of the object at time t.
• x0 is the initial displacement of the object at time t=0.
• v0 is the upward velocity with which the object was thrown.
• g is the acceleration due to gravity (9.8 m/s^2 on the surface of the Earth).
• t is the time elapsed.

Equation of motion of a body moving with constant acceleration along straight line

 

 The equation of motion of a body moving with constant acceleration along a straight line can be derived from Newton's second law of motion, which states that the acceleration of an object is proportional to the force acting on it and inversely proportional to its mass.

Let's consider a body moving with constant acceleration along a straight line and let's call the initial velocity of the body at time t=0 as v0, the final velocity of the body at time t as v, the constant acceleration of the body as a, the time elapsed as t and the displacement of the body as x.

The first equation we can derive is the velocity equation:

v = v0 + at

This equation states that the final velocity of the body at time t is equal to its initial velocity plus the product of its acceleration and time. This means that if the body was initially at rest (v0 = 0), its velocity will increase linearly with time as long as the acceleration remains constant. If the acceleration is positive, the velocity of the body will increase and if the acceleration is negative, the velocity of the body will decrease.

Next, we can derive the displacement equation:

x = x0 + v0t + (1/2)at^2 (Check the image for the exact formula)

This equation states that the final displacement of the body at time t is equal to its initial displacement plus the product of its initial velocity and time plus half of the product of its acceleration and the square of time. This equation takes into account the change in velocity of the body over time and the distance traveled during that change.

Define rest & motion, speed & velocity, displacement & distance, uniform & non-uniform speed & velocity, instantaneous velocity, acceleration

Kinematics is the branch of mechanics that deals with the motion of objects without considering the forces that cause the motion.

Rest and Motion: 

• An object is said to be at rest if its position relative to its surroundings does not change over time. 
• If its position changes, it is said to be in motion.
  

Speed and Velocity: 

• Speed is a scalar quantity that measures the magnitude of an object's change in position (distance) per unit of time. 
• Velocity is a vector quantity that includes both the speed and direction of an object's change in position.

Displacement and Distance: 

• Displacement is a vector quantity that measures the change in position of an object from its initial to final position. 
• Distance is a scalar quantity that measures the total length of the path taken by an object from its initial to final position.

Uniform and Non-Uniform Speed/Velocity: 

• An object is said to have uniform speed if its speed is constant over time. 
• An object is said to have non-uniform speed if its speed changes over time. 
• The same applies to velocity, an object is said to have uniform velocity if both its speed and direction remain constant over time and non-uniform velocity if either its speed or direction changes over time.

Instantaneous Velocity: 

• The velocity of an object at a specific instant in time. It can be thought of as the limit of the average velocity over a very short period of time as the time interval approaches zero.

Acceleration:

• Acceleration is the rate of change of velocity over time, and it is a vector quantity that measures the change in the direction or magnitude of an object's velocity.